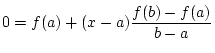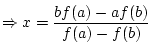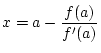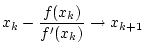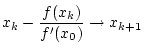Nichtlineare
Gleichungssysteme, Nullstellen
Allgemeine Problemstellung
Gegeben sei eine Funktion
Es ist nun eine Stelle
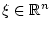 gesucht, so dass gesucht, so dass
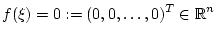 |
(1) |
ist. Eine solche Stelle 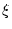 heißt
Nullstelle der Funktion heißt
Nullstelle der Funktion 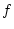 . .
Problem (1) ist äquivalent zu
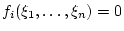 für
für 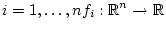 |
(2) |
Das System (2) nennt man ein
nichtlineares Gleichungssystem.
Ist dagegen zusätzlich noch ein Vektor 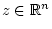 gegeben, und möchte man dann das allgemeine Problem
lösen, ein
gegeben, und möchte man dann das allgemeine Problem
lösen, ein
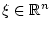 zu bestimmen, so dass
so kann man zu bestimmen, so dass
so kann man
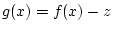 setzen. Dann gilt
Es reicht also, ohne Einschränkung, Nullstellen einer Funktion
bestimmen zu können. Wie bestimmt man aber nun ein solches setzen. Dann gilt
Es reicht also, ohne Einschränkung, Nullstellen einer Funktion
bestimmen zu können. Wie bestimmt man aber nun ein solches
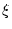 ? ?
Einteilung der Verfahren
Schon von Polynomen mit einem Grad größer als 4 lassen
sich die Nullstellen im Allgemeinen nicht mehr exakt bestimmen. Man
versucht also nun eine Näherung 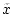 der
tatsächlichen Nullstelle der
tatsächlichen Nullstelle 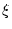 zu berechnen.
Allen Verfahren ist somit gemein, dass sie sich, ausgehend von
einem oder mehreren Startwerten, (hoffentlich) immer mehr einer
Lösung von (1) annähern. Man kann
die Verfahren jedoch nach folgenden Kriterien unterscheiden: zu berechnen.
Allen Verfahren ist somit gemein, dass sie sich, ausgehend von
einem oder mehreren Startwerten, (hoffentlich) immer mehr einer
Lösung von (1) annähern. Man kann
die Verfahren jedoch nach folgenden Kriterien unterscheiden:
Die Verfahren im R1
Fixpunktiteration
Das Verfahren der Fixpunktiteration wird benutzt um eine
Lösung der skalaren Gleichung 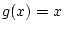 zu
finden. Will man dagegen die Nullstelle einer Funktion zu
finden. Will man dagegen die Nullstelle einer Funktion
 finden, so definiert man finden, so definiert man
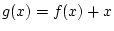 und die Nullstelle von und die Nullstelle von
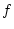 ist Fixpunkt von ist Fixpunkt von 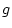 . .
Das Verfahren besteht darin, einen Wert in 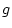 einzusetzen, und dies mit dem Ergebnis zu wiederholen, usw....
Formal ergibt sich der Algorithmus
einzusetzen, und dies mit dem Ergebnis zu wiederholen, usw....
Formal ergibt sich der Algorithmus
- INIT: Gegeben sei
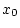
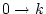 -
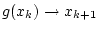
- FALLS
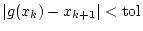
 RETURN RETURN 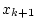
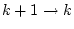 - WEITER bei 3.
Der Banachsche Fixpunktsatz gibt an unter welchen Bedingungen das
Verfahren konvergiert:
Sei 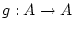 eine kontrahierende Abbildung, d.h.
mit einem eine kontrahierende Abbildung, d.h.
mit einem 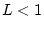 , auf einer abgeschlossenen
Teilmenge , auf einer abgeschlossenen
Teilmenge 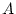 eines Banach-Raumes. Dann konvergiert
das Verfahren für alle Startwerte eines Banach-Raumes. Dann konvergiert
das Verfahren für alle Startwerte 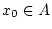 gegen
den eindeutig bestimmten Fixpunkt gegen
den eindeutig bestimmten Fixpunkt 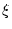 von von
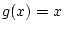 . .
Das Bisektions- oder
Intervallhalbierungsverfahren
Das Bisektionsverfahren wird verwandt um Nullstellen einer skalaren
Funktion
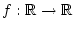 zu bestimmen. Vorgegeben werden
müssen zwei Stellen zu bestimmen. Vorgegeben werden
müssen zwei Stellen 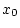 und und 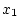 , so dass
, so dass
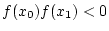 (d.h. die beiden
Funktionswerte von (d.h. die beiden
Funktionswerte von  haben unterschiedliches
Vorzeichen). Also liegt zwischen haben unterschiedliches
Vorzeichen). Also liegt zwischen 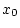 und und 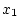 mindestens eine Nullstelle. Als neue Näherung wird
dann die Mitte des Intervalls mindestens eine Nullstelle. Als neue Näherung wird
dann die Mitte des Intervalls ![$ [x_0,x_1]$](nullstellen_text_files/img41.png) verwandt:
Je nachdem welches Vorzeichen nun verwandt:
Je nachdem welches Vorzeichen nun 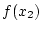 hat,
wird das Verfahren nun erneut entweder auf das linke oder im auf
das rechte Teilintervall angewandt. Abgebrochen wird, falls das
Intervall in dem die Nullstelle sicher liegt hinreichend klein
geworden ist. hat,
wird das Verfahren nun erneut entweder auf das linke oder im auf
das rechte Teilintervall angewandt. Abgebrochen wird, falls das
Intervall in dem die Nullstelle sicher liegt hinreichend klein
geworden ist.
- INIT: Gegeben ist ein Intervall
![$ [a, b]$](nullstellen_text_files/img44.png) mit mit
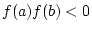
-
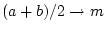
- FALLS
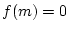
 RETURN RETURN 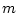
- FALLS
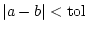
 RETURN RETURN 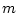
- FALLS
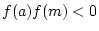
 DANN WEITER bei 1. mit DANN WEITER bei 1. mit ![$ [a,m]$](nullstellen_text_files/img51.png)
 SONST WEITER bei 1. mit SONST WEITER bei 1. mit ![$ [m,b]$](nullstellen_text_files/img52.png)
Das Verfahren konvergiert unter den gegebenen Voraussetzungen immer
gegen eine Nullstelle 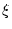 . .
Regula Falsi
Achtung: Hier gilt Regula Falsi 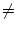 Sekantenverfahren, an anderen Stellen könnten abweichende
Bezeichnungen verwandt werden!
Sekantenverfahren, an anderen Stellen könnten abweichende
Bezeichnungen verwandt werden!
Regula Falsi wird verwandt um Nullstellen einer skalaren Funktion
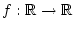 zu bestimmen. Das Verfahren ist
identisch zum Bisektionsverfahren, nur wird nicht einfach die Mitte
des Intervalls verwandt, sondern es wird die Nullstelle der
interpolierenden Geraden durch zu bestimmen. Das Verfahren ist
identisch zum Bisektionsverfahren, nur wird nicht einfach die Mitte
des Intervalls verwandt, sondern es wird die Nullstelle der
interpolierenden Geraden durch
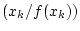 und und
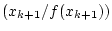 verwandt: verwandt:
- INIT: Gegeben ist ein Intervall
![$ [a, b]$](nullstellen_text_files/img44.png) mit mit
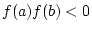
-
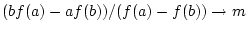
- FALLS
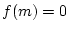
 RETURN RETURN 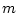
- FALLS
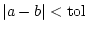
 RETURN RETURN 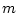
- FALLS
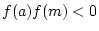
 DANN WEITER bei 1. mit DANN WEITER bei 1. mit ![$ [a,m]$](nullstellen_text_files/img51.png)
 SONST WEITER bei 1. mit SONST WEITER bei 1. mit ![$ [m,b]$](nullstellen_text_files/img52.png)
Das Verfahren konvergiert unter den gegebenen Voraussetzungen immer
gegen eine Nullstelle 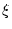 . .
Sekantenverfahren
Achtung: Hier gilt Regula Falsi 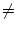 Sekantenverfahren, an anderen Stellen könnten abweichende
Bezeichnungen verwandt werden!
Sekantenverfahren, an anderen Stellen könnten abweichende
Bezeichnungen verwandt werden!
Das Sekantenverfahren wird verwandt um Nullstellen einer skalaren
Funktion
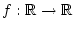 zu bestimmen. Verzichtet man in
der Regula Falsi auf die Forderung von verschiedenen Vorzeichen an
den Enden des jeweiligen Intervalls, erhält man das
Sekantenverfahren: zu bestimmen. Verzichtet man in
der Regula Falsi auf die Forderung von verschiedenen Vorzeichen an
den Enden des jeweiligen Intervalls, erhält man das
Sekantenverfahren:
- INIT: Gegeben sind
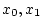 mit mit
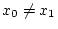
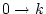 -
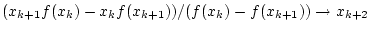
- FALLS
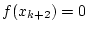
 RETURN RETURN 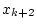
- FALLS
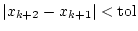
 RETURN RETURN 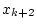
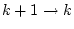 - WEITER bei 3.
Das Verfahren ist nicht stabil, falls in Schritt 3.
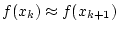 gilt, und daher ist
die Konvergenz nicht immer garantiert, es besitzt aber lokal in
einer hinreichend kleinen Umgebung der Nullstelle die
Konvergenzordnung gilt, und daher ist
die Konvergenz nicht immer garantiert, es besitzt aber lokal in
einer hinreichend kleinen Umgebung der Nullstelle die
Konvergenzordnung
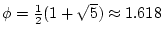 . .
Newton Verfahren
Das Newton-Verfahren wird verwandt um Nullstellen einer skalaren
Funktion
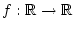 zu bestimmen. Dabei muss zu bestimmen. Dabei muss
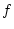 mindestens einmal stetig differenzierbar
sein. mindestens einmal stetig differenzierbar
sein.
Das Newton-Verfahren kann als Verbesserung der Sekantenmethode
angesehen werden, nur wird dabei die Sekante durch eine Tangente
ersetzt. Aus der Tangentengleichung
ergibt sich aus  die Vorschrift:
Dies führt zu folgendem Verfahren: die Vorschrift:
Dies führt zu folgendem Verfahren:
- INIT: Gegeben sei
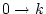 -
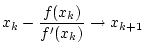
- FALLS
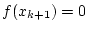
 RETURN RETURN 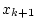
- FALLS
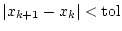
 RETURN RETURN 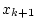
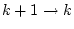 - WEITER bei 3.
In Schritt 3. kann eine Division durch 0 auftreten, falls
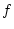 an der Stelle an der Stelle 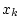 eine
waagerechte Tangente besitzt. Das Verfahren bricht dann erfolglos
ab. eine
waagerechte Tangente besitzt. Das Verfahren bricht dann erfolglos
ab.
Das Newton Verfahren ist für eine einfache Nullstelle, und
falls 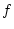 dreimal stetig differenzierbar ist, in einer
hinreichend kleinen Umgebung der Nullstelle mindestens quadratisch
konvergent. dreimal stetig differenzierbar ist, in einer
hinreichend kleinen Umgebung der Nullstelle mindestens quadratisch
konvergent.
Vereinfachtes Newton
Verfahren
Um nicht in jedem Schritt 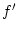 auswerten zu
müssen (teuer), kann man den Wert von auswerten zu
müssen (teuer), kann man den Wert von 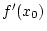 in
den folgenden Iterationen weiterbenutzen, wenn man annimmt dass
dieser eine gute Näherung der folgenden in
den folgenden Iterationen weiterbenutzen, wenn man annimmt dass
dieser eine gute Näherung der folgenden
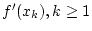 darstellt. Dies führt
zu folgendem Verfahren: darstellt. Dies führt
zu folgendem Verfahren:
- INIT: Gegeben sei
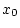
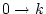 -
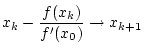
- FALLS
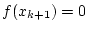
 RETURN RETURN 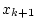
- FALLS
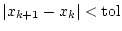
 RETURN RETURN 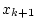
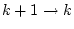 - WEITER bei 3.
Das vereinfachte Newton Verfahren konvergiert allerdings nur noch
linear.
Das mehrdimensionale Newton-Verfahren
Das mehrdimensionale Newton-Verfahren wird benutzt um Nullstellen 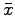 von Funktionen
von Funktionen
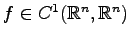 zu
bestimmen. Hierbei muss
zu
bestimmen. Hierbei muss
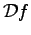 invertierbar sein.
invertierbar sein.
Es ist die folgende Gleichung zu lösen:
Man erhält das lineare Gleichungssystem
Dieses wird numerisch gelöst. Dann ergibt sich 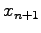 aus
aus
Verfahren von Muller
Eine weitere Verallgemeinerung des Sekantenverfahrens stellt das
Verfahren von Muller dar. Dabei wird nicht durch 2 Punkte eine
Sekante gelegt, sondern durch 3 Punkte eine interpolierende
Parabel. Das führt zu folgendem Algorithmus:
- INIT: Gegeben sind
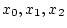 paarweise verschieden paarweise verschieden
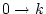 - Bestimme eine Parabel
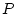 durch die Punkte durch die Punkte
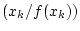 , ,
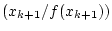 und und
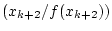 . .
- FALLS
 keine reelle Nullstelle besitzt keine reelle Nullstelle besitzt
 RETURN "`Fehler"' RETURN "`Fehler"'
- Die Nullstelle die am dichtesten bei
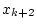 liegt
liegt 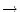 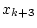 . .
- FALLS
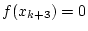
 RETURN RETURN 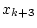
- FALLS
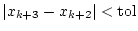
 RETURN RETURN 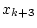
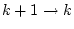 - WEITER bei 3.
|