Interpolation

 Allgemeines Interpolationsproblem

Interpolation bedeutet vereinfacht: Eine Funktion zu bestimmen, die durch gegebene Datenpaare verläuft.

Wir gehen davon aus, dass reelle Datenpaare

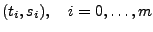
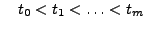
$\displaystyle ( t_i ,s_i ) , i=0, \hdots, m$   mit$\displaystyle \quad t_0 < t_1 < \hdots < t_m$

gegeben sind und eine reelle Funktion 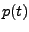$ p(t)$ gesucht wird mit

$\displaystyle p( t_i )= s_i,\quad i=0, \hdots, m.$

Die Daten können Daten aus einem Tafelwerk sein oder - wichtiger - approximative Funktionsdaten, die selbst aus einer numerischen Rechnung kommen. Wenn die Daten nicht von einer glatten Funktion stammen sondern aus Messergebnissen, so ist die Suche nach einer Interpolationsfunktion sehr fragwürdig (siehe Käferpopulation).

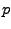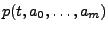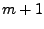Sinnvoll ist die Interpolationsaufgabe nur, wenn $ p$ in einer Familie von Funktionen $ p( t , a_0 , \hdots , a_m )$ gesucht wird, die von $ m+1$ freien Parametern abhängt. Dann sind 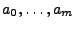$ a_0 , \hdots , a_m$ zu bestimmen, so dass

$\displaystyle p( t_i , a_0 , \hdots , a_m )= s_i,\quad i=0,\hdots, m$

gilt. Dies ist das allgemeine Interpolationsproblem.

 

 Interpolation mit Polynomen

Ein Beispiel einer Familie von Funktionen, die von 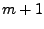$ m+1$ Parametern abhängen, sind die Polynome vom Grad $ m$.

$\displaystyle p( t , a_0 , \hdots , a_m )= a_m t^m + a_{m-1}t^{m-1} + \hdots + a_0$

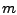Man spricht dann von einer Polynom-Interpolation.

Das folgende Programm führt die Polynom-Interpolation aus. Die Datenpaare können per Hand in eine Liste eingegeben werden oder durch Auswertung einer Funktion erfolgen.

 

 Interpolation mit Spline

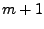
Ein weitere Gruppe von Funktionen, die von $ m+1$ Parametern abhängen, sind die so genannten Splines. Der Einfachheit halber wird sich im Folgenden auf den Fall der kubischen Splines beschränkt.

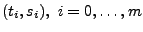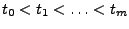Wir gehen wieder von den obigen Datenpaaren $ ( t_i ,s_i ), i=0, \hdots, m$ mit $ t_0 < t_1 < \hdots < t_m$ aus.

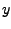Ein zu der obigen Zerlegung des Intervalls $ [t_0 , t_m]$ gehöriger kubischer Spline ist eine reelle Funktion $ y$ mit den Eigenschaften:

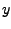  1. $ y$ ist auf $ [t_0 , t_m]$ zweimal stetig differenzierbar.
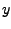  2. Auf jedem Teilintervall $ [t_i , t_{i+1}], i=0, \hdots, m-1$ stimmt $ y$ mit einem Polynom dritten Grades überein.
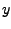
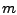
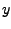
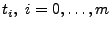
Ein Spline $ y$ ist somit stückweise aus $ m$ kubischen Polynomen so zusammengesetzt, dass die Funktion $ y$ selbst und ihre beiden ersten Ableitungen an den Knoten $ t_i , i=0, \hdots, m$ keine Sprungstellen besitzen.

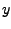Sei im Folgenden $ p_i := y\vert _{[t_i , t_{i+1}]}, i=0, \hdots, m-1$ die zum Spline $ y$ gehörigen kubischen Polynome. Im Gegensatz zu der Polynominterpolation werden dies Polynome nur auf den entsprechenden Teilintervallen benötigt.

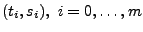Mit der Forderung, dass der Spline durch die Punkte $ ( t_i ,s_i ), i=0, \hdots, m$ gehen soll, erhält man:

  • $ p_i ( t_i ) = s_i,\quad i=0, \hdots, m-1$
  • $ p_i ( t_{i+1} ) = s_{i+1},\quad i=0, \hdots, m-1$

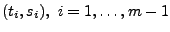Da der Spline zweimal stetig differenzierbar sein soll, erhält man für die "'inneren"' Punkte $ ( t_i ,s_i ), i=1, \hdots, m-1$ die folgende Forderungen:

  • $ p_{i-1}'( t_i ) = p_i'( t_i ),\quad i=1, \hdots, m-1$
  • $ p_{i-1}''( t_i ) = p_i''( t_i ),\quad i=1, \hdots, m-1$

An den Rändern fordern wir zunächst:

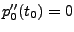
  1. $ p_0''( t_0 ) = 0$
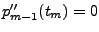
  2. $ p_{m-1}''( t_m ) = 0$

Man kann zeigen, dass sich daraus alle kubischen Polynome des Splines eindeutig bestimmen lassen. Somit ist der Spline 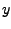$ y$ in Abhängigkeit von den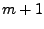 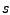$ m+1$ $ s$-Werten eindeutig; also:

$\displaystyle y( t ) = y( t , s_0 , \hdots , s_m ).$

Ein Spline 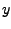$ y$, der die obige Forderung

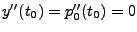
  1. $ y''( t_0 ) = p_0''( t_0 ) = 0$
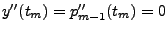
  2. $ y''( t_m ) = p_{m-1}''( t_m ) = 0$
erfüllt, wird natürlicher Spline genannt.

Neben den natürlichen Splines gibt es noch weitere Gruppen. Erfüllen die Daten zusätzlich 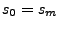$ s_0 = s_m$

werden häufig statt den Gleichungen I. und II., also 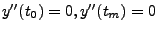$ y''( t_0 ) = 0, y''( t_m ) = 0$, die Forderungen

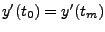
  1. $ y'( t_0 ) = y'( t_m )$
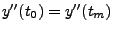
  2. $ y''( t_0 ) = y''( t_m )$

aufgestellt. Man kann zeigen, dass der Spline auch unter diesen Forderungen eindeutig bestimmt ist. Falls der Spline die Forderungen III. und IV. erfüllt, spricht man von einem periodischen Spline.

Eine weitere Gruppe von Splines ist durch die Forderung

  1. $ y'( t_0 ) = a$
  2. $ y'( t_m ) = b$

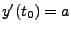
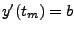
eindeutig bestimmt, wobei 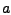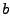$ a$, $ b$ zwei vorher festgelegte reelle Zahlen sind.

Wird das allgemeine Interpolationsproblem mittels eines Splines gelöst, so spricht man dementsprechend von einer Spline-Interpolation.

Das folgende Programm führt die Spline-Interpolation aus. Dabei wird ein natürlicher Spline bestimmt. Die Datenpaare können per Hand in eine Liste eingegeben werden oder durch Auswertung einer Funktion erfolgen.