Die
Romberg Integration beruht auf
der oben vorgestellten Trapezsumme. Man kann zeigen, dass für
die Trapezsumme einer
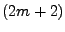
-mal stetig
differenzierbaren Funktion folgende Fehlerdarstellung gilt:
wobei
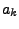
von
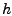
unabhängige
Konstanten sind. Insbesondere ist der Fehler bei der Trapezsumme
vom Typ
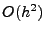
. Eine Herleitung des Romberg
Verfahrens besteht darin die Faktoren
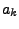
durch
geschickte Addition zu eliminieren und so die Fehlerordnung zu
erhöhen.
Dazu werden zunächst die Treppensummen
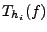 für
für
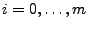 mit
mit
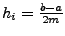 bestimmt. Nun wird das
folgende Romberg-Schema angewandt:
bestimmt. Nun wird das
folgende Romberg-Schema angewandt:
Dabei ergibt sich
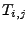
durch die folgende
Additionsformel:
Damit lässt sich zeigen, dass in jeder Spalte die Ordnung des
Fehlers um 2 erhöht wird, in der
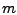
-ten Spalten
also ein Fehler vom Typ
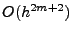
vorliegt.
Man kann ebenso zeigen, dass die zweite Spalte der Simpsonsumme
entspricht, d.h. 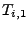 entspricht der Simpsonsumme
zur Weite
entspricht der Simpsonsumme
zur Weite 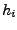 .
.
Das folgende Programm führt die Rombergintegration aus. Man
kann Spalten aus dem obigen Rombergschema auswählen und sich
den jeweiligen Fehler zum exakten Integral anzeigen lassen.
Außerdem kann man sich den Fehler der Diagonalen, d.h. von
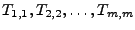 ausgeben
lassen.
ausgeben
lassen.
Adaptive Integration
Die Romberg Integration liefert bei
glatten Funktionen sehr gute Approximationen an das Integral.
Jedoch bei stark variierenden Funktionen ist die Romberg
Integration eher ineffektiv. Man würde dann lieber nicht
äquidistante Stützstellen je nach dem Verhalten von
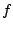
verwenden. Diesen Ansatz verfolgt die
adaptive Integration.
Zur Erläuterung des Verfahrens wird das folgende
Teilintervall
![$ [ x_i , x_{i+1} ]$](Integration_text_files/img37.png) betrachtet. Auf diesem
Intervall wird sowohl die Treppensumme
betrachtet. Auf diesem
Intervall wird sowohl die Treppensumme 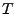 , als auch die
Simpsonregel
, als auch die
Simpsonregel 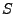 berechnet. Anschließend wird
geprüft, ob folgende Bedingung erfüllt ist.
berechnet. Anschließend wird
geprüft, ob folgende Bedingung erfüllt ist.
Hierbei ist
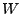
ein sehr grober Schätzwert
für das exakte Integral, welcher die Größenordnung
erfasst, und
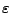
die geforderte relative
Genauigkeit. Wird die obige Bedingung erfüllt, so wird
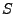
als Approximation auf diesem Teilintervall
akzeptiert und das nächste Teilintervall betrachtet.
Wird die obige Bedingung nicht erfüllt, so wird das
Intervall
![$ [ x_i , x_{i+1} ]$](Integration_text_files/img37.png) in die zwei Teilintervalle
in die zwei Teilintervalle
![$ [ x_i , \tau ]$](Integration_text_files/img43.png) und
und
![$ [ \tau , x_{i+1} ]$](Integration_text_files/img44.png) aufgeteilt, wobei
aufgeteilt, wobei
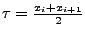 ist.
Anschließend wird diese Methode zunächst auf das
Intervall
ist.
Anschließend wird diese Methode zunächst auf das
Intervall
![$ [ x_i , \tau ]$](Integration_text_files/img43.png) und dann auf das Intervall
und dann auf das Intervall
![$ [ \tau , x_{i+1} ]$](Integration_text_files/img44.png) angewendet.
angewendet.
Das folgende Programm führt die adaptive Integration aus.
Man kann sowohl die relative Genauigkeit
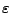 , als auch die maximale Anzahl an
Stützstellen angeben. Anschließend wird die Bestimmung
der Stützstellen als Slideshow angezeigt.
, als auch die maximale Anzahl an
Stützstellen angeben. Anschließend wird die Bestimmung
der Stützstellen als Slideshow angezeigt.