Fortsetzung (Continuation) von Nullstellen
Gegeben sei die Funktion
Es wird eine Nullstellenkurve von 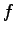 gesucht. Wir bestimmen diese
Kurve mit der Pseudobogenlängen-Fortsetzung.
gesucht. Wir bestimmen diese
Kurve mit der Pseudobogenlängen-Fortsetzung.
Als erstes muss die zu betrachtende Funktion 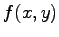 vom Benutzer eingegeben
werden. Danach sollte der Startwert (initial point) und eine Schätzung des
Tangentialvektors (psi) in die GUI eingetragen werden. Die maximale
Anzahl der Fortsetzungsschritte wird unter
vom Benutzer eingegeben
werden. Danach sollte der Startwert (initial point) und eine Schätzung des
Tangentialvektors (psi) in die GUI eingetragen werden. Die maximale
Anzahl der Fortsetzungsschritte wird unter 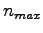 eingegeben. Hierbei
ist zu beachten, dass die Fortsetzung abbricht, falls der
Bildrand in weniger als
eingegeben. Hierbei
ist zu beachten, dass die Fortsetzung abbricht, falls der
Bildrand in weniger als 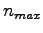 Schritten erreicht wird. Danach ist eine
weitere Fortsetzung mittels des Knopfes
Schritten erreicht wird. Danach ist eine
weitere Fortsetzung mittels des Knopfes 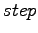 und der dahinter
eingetragenen Schrittzahl möglich.
und der dahinter
eingetragenen Schrittzahl möglich.
Als nächstes werden die Schrittweiten :
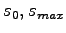
und
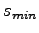
benötigt. Für die Schrittweitensteuerung werden zusätzlich die
Dämpfungsfaktoren 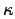 und
und 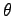 gebraucht (vgl. Abbildung 1).
Der Parameter
gebraucht (vgl. Abbildung 1).
Der Parameter 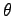 wird auch im Newtonblock (vgl. Abbildung 2)
genutzt. Die maximale Anzahl der Newtonschritte wird mit dem Parameter
wird auch im Newtonblock (vgl. Abbildung 2)
genutzt. Die maximale Anzahl der Newtonschritte wird mit dem Parameter
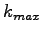 festgelegt. Der Parameter
festgelegt. Der Parameter 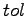 gibt die Toleranz des Newtonverfahrens an.
gibt die Toleranz des Newtonverfahrens an.
Nach Durchführung des Verfahrens wird eine glatte Kurve aus
den berechneten Daten mittels kubischer Interpolation bestimmt,
vgl. Kapitel 3.3 in [2].
Die Details des Algorithmus der Pseudobogenlängen-Fortsetzung
können in ![$ [1]$](continuation_text_files/img12.png) nachgelesen
werden.
nachgelesen
werden.
Die folgenden Abbildungen zeigen den in der GUI eingesetzten
Algorithmus sowie den Newtonblock.
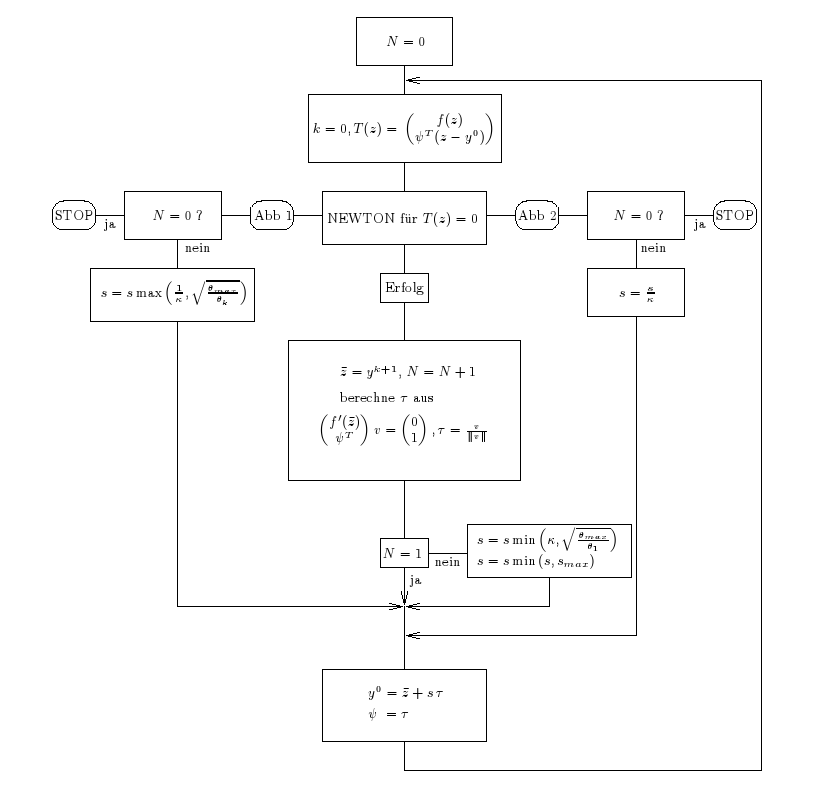
Abbildung 1: Pseudobogenlängen-Fortsetzung
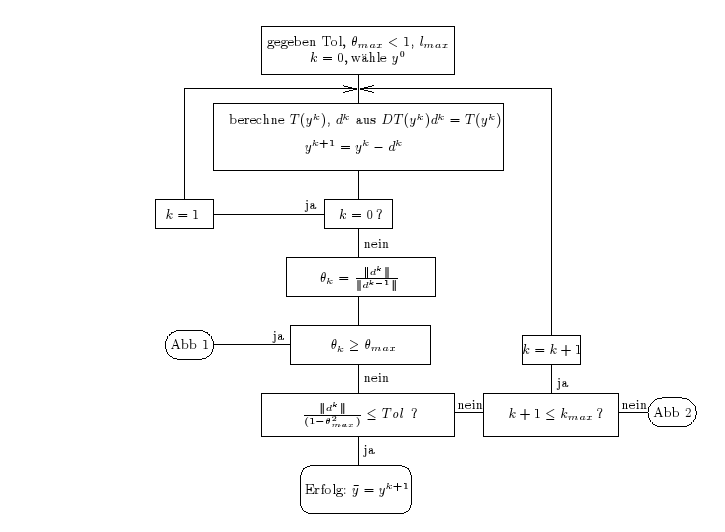
Abbildung 2: Newtonblock
Die Abbildungen 1 und 2 wurden aus [3] entnommen.
[1] Willy J.F. Govaerts. Numerical methods for bifurcations of
dynamical equilibria.
Society for Industrial and Applied Mathematics (SIAM),
Philadelphia, PA, 2000
[2] W.-J. Beyn. Vorlesungsskriptum Numerik I. Universität Bielefeld,
Sommersemester 2006
[3] J. Möller. Das nichtlineare Eigenwertproblem, Bielefeld, 07.03.2008

