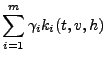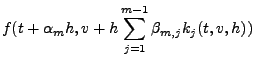Differentialgleichungen

 Übersicht

Anfangswertaufgabe Erläuterung
Allgemeines über Einschrittverfahren Erläuterung
Euler Verfahren Erläuterung
implizites Euler Verfahren Erläuterung
Verfahren von Heun Erläuterung
Runge-Kutta Verfahren Erläuterung

 

 

 

 

 

 Anfangswertaufgabe

Das folgende Programm löst numerisch ein System von $ n$ Anfangswertaufgaben in der Form

$\displaystyle u'(t) = f(t,u(t)),\,\, t \in [t_0, t_{end}],\,\, u(t_0) = u_0 \in \mathbb{R}^n$
wobei
$\displaystyle u(t) = (u_1(t), \hdots, u_n(t)) $ bzw. $\displaystyle u'(t) = (u'_1(t), \hdots, u'_n(t))$
die gesuchte Vektorfunktion bzw. der Vektor der Ableitungen ist und $ f$ eine Funktion der Form
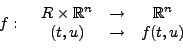
\begin{displaymath}\begin{array}{cc} f:& \begin{array}{ccc} R \times \mathbb{R... ...to& \mathbb{R}^n \ (t,u) &\to& f(t,u) \end{array}\end{array}\end{displaymath}
ist.

Zur Lösung dieses Problems wurden verschiedene numerische Verfahren entwickelt. Im Folgenden werden einige ausgewählte Einschrittverfahren näher vorgestellt.

 

 Top

 

 

 

 

 Allgemeines über Einschrittverfahren

Bei den Einschrittverfahren wird zunächst eine Schrittweite $ h$ gewählt. Mittels dieser Schrittweite wird dann auf dem Intervall $ [t_0, t_{end}]$ das äquidistante Gitter

$\displaystyle \Omega_h := R_h \cap [t_0, t_{end}]$    mit $\displaystyle R_h := \{t_0+jh : j \in\N \}$
definiert. Ausgehend vom ersten Gitterpunkt $ t_0$ dem Anfangswert $ u_0=u(t_0)$ berechnen die hier vorgestellten Einschrittverfahren eine Approximation $ u_1$ für $ u(t_1)$, also den Wert der Vektorfunktion am zweiten Gitterpunkt. Anschließend wird ausgehend vom Tupel $ (t_1,u_1)$ eine Approximation $ u_2$ an den Wert $ u(t_2)$ berechnet. Dieses Vorgehen wird dann iteriert, bis für alle Gitterpunkte eine Approximation $ u_j$ an $ u(t_j)$ berechnet wurden. Anschaulich bedeutet dies:
\begin{displaymath} \begin{array}{l} (t_0,u_0) \stackrel{ESV}{\longrightarrow} ... ...d}) \ \ ESV = \mbox{ Einschrittverfahren} \ \end{array}\end{displaymath}

Ein möglicher Ausgangspunkt zum Verständnis der Einschrittverfahren ist die Methode der vorwärtsgenommenen Differenzenquotienten: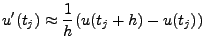
An einem Punkt $ t_j$ kann man die Ableitung $ u'(t_j)$ durch folgenden Term approximieren:

$\displaystyle u'(t_j) \approx \frac{1}{h} ( u(t_j+h) - u(t_j) )$

Da die Lösung $ u'(t_j) = f(t_j,u(t_j))$ erfüllt, wird nun die linke Seite in der obigen Formel durch $ f(t_j,u(t_j))$ ersetzt und Gleichheit angenommen. Durch Auflösung nach $ u(t_{j+1})$ erhält man:

$\displaystyle u(t_{j+1}) = u(t_j) + h f(t_j,u(t_j))$ (1)

Dies führt zum Euler-Verfahren, das im folgenden Abschnitt näher beschrieben wird.

Dieser Ansatz wird nun verallgemeinert, indem in der Gleichung % latex2html id marker 575 $ (\ref{simple})$ die Funktion $ f$ durch eine allgemeinere Funktion $ \varphi$ ersetzt wird. Damit erhält man ein allgemeines Einschrittverfahren der Form:

$\displaystyle u(t_{j+1}) = u(t_j) + h \varphi(t_j,u(t_j),h)$ (2)

Man nennt die Funktion $ \varphi$ Verfahrensfunktion oder Inkrementfunktion.

Um die Güte der unterschiedlichen Verfahren vergleichen zu können, wird der Konsistenzfehler bzw. der lokale Diskretisierungsfehler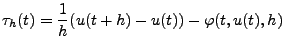

$\displaystyle \tau_h(t) = \frac{1}{h} ( u(t+h) - u(t) ) - \varphi(t,u(t),h)$

betrachtet, wobei $ u: \mathbb{R} \to \mathbb{R}^n$ die exakte Lösung der Anfangswertaufgabe ist.

Dann heißt ein Einschrittverfahren konsistent bzw. konsistent von der Ordnung $ p$, wenn für $ h \to 0$ gilt:

$\displaystyle \tau_h(t) \to 0$$\displaystyle \mbox { bzw. } \tau_h(t) = O(h^p)$

Ein Einschrittverfahren heißt konvergent bzw. konvergent von der Ordnung $ p$, wenn für $ h \to 0$ gilt:

$\displaystyle \vert\vert u_h(t)-u(t)\vert\vert \to 0$    bzw. $\displaystyle \vert\vert u_h(t)-u(t)\vert\vert = O(h^p) \forall t \in \Omega_h$

wobei $ u_h$ die numerische Lösung auf dem Gitter $ \Omega_h$ ist.

 

 Top

 

 

 

 

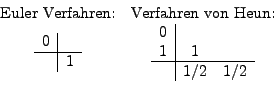
 Euler Verfahren

Das einfachste numerische Verfahren zur Lösung einer Anfangswertaufgabe ist das bereits erwähnte Euler-Verfahren, auch Polygonzugverfahren genannt.

Beim Euler-Verfahren wird die folgende Verfahrensfunktion benutzt:

$\displaystyle \varphi(t,v,h) = f(t,v)$

Man erhält also aus der Gleichung % latex2html id marker 610 $ (\ref{better})$ das Verfahren:

$\displaystyle u(t_{j+1}) = u(t_j) + h f(t_j,u(t_j))$

Diese Gleichung impliziert den folgenden Algorithmus:

  1. $ j=0$
  2. $ t_{j+1} = t_j + h$
  3. Wenn $ t_{j+1} > t_{end}$ dann STOP, sonst weiter bei Schritt 4
  4. $ u_{j+1}=u_j + h f(t_j,u_j)$
  5. $ j=j+1$ und weiter bei Schritt 2

Dies ist das Euler-Verfahren. Man kann zeigen, dass dieses Verfahren konsistent von der Ordnung 1 ist.

 

 Top

 

 

 

 

 implizites Euler Verfahren

Das implizite Euler-Verfahren wird durch die folgende Gleichung beschrieben:

$\displaystyle u(t_{j+1})=u(t_j) + h f(t_{j+1},u(t_{j+1})).$

Diese Gleichung impliziert den folgenden Algorithmus:
$\displaystyle 1.$   $\displaystyle j=0$  
$\displaystyle 2.$   $\displaystyle t_{j+1} = t_j+h$  
$\displaystyle 3.$   Wenn $\displaystyle t_{j+1} > t_{end}$    dann STOP, sonst weiter bei Schritt 4  
$\displaystyle 4.$   Finde Nullstelle von $\displaystyle g(u):= u - u_j - h f(t_{j+1},u)$    mit dem Newton Verfahren.  
$\displaystyle 5.$   $\displaystyle u_{j+1}= u$  
$\displaystyle 6.$   $\displaystyle j=j+1$    und weiter bei Schritt 2  

 

 Top

 

 

 

 

 Methode von Heun

Beim Euler-Verfahren wird nur ein sehr eingeschränkter Gebrauch vom Richtungsfeld der Differentialgleichung gemacht. Es wird nur die Richtung des aktuellen Punktes $ (t_j,u_j)$ ausgewertet. Die Idee ist nun in einer Umgebung des Punktes $ (t_j,u_j)$ das Richtungsfeld an mehreren Punkten abzutatsten.

Ein Ansatz verwendet z.B. das arithmetische Mittel der Steigungen $ f(t_j,u_j)$ und $ f(t_j+h,u_j+hf(t_j,u_j))$ zu verwenden. Dies führt auf die folgende Verfahrensfunktion:

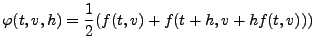
$\displaystyle \varphi(t,v,h) = \frac{1}{2} ( f(t,v) + f(t+h, v+h f(t,v)) )$

Man erhält also aus der Gleichung % latex2html id marker 635 $ (\ref{better})$ die Vorschrift

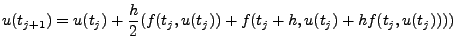
$\displaystyle u(t_{j+1}) = u(t_j) + \frac{h}{2} (f(t_j,u(t_j)) + f(t_j+h,u(t_j)+h f(t_j,u(t_j))) )$

und damit den folgenden Algorithmus:

  1. $ j=0$
  2. $ t_{j+1} = t_j + h$
  3. Wenn $ t_{j+1} > t_{end}$ dann STOP, sonst weiter bei Schritt 4
  4. $ k = f(t_j,u_j)$
  5. $ u_{j+1} = u_j+\frac{h}{2}(k + f(t_j+1,u_j+hk) )$
  6. $ j=j+1$ und weiter bei Schritt 2

Dies ist das sogenannte Verfahren von Heun.

Man sieht sofort, dass dieser Algorithmus gegenüber dem Euler-Verfahren eine zusätzliche Auswertung der Funktion $ f$ benötigt. Jedoch kann man zeigen, dass das Verfahren von Heun konsistent von der Ordnung 2 ist.

 

 Top

 

 

 

 

 Runge-Kutta-Verfahren

Beim allgemeinen Runge-Kutta Verfahren wird der beim Verfahren von Heun vorgestellte Ansatz weiter verallgemeinert indem man die Funktion $ f$ an mehreren verschobenen Stellen auswertet. Dies ergibt dann folgende allgemeine Verfahrensfunktion $ \varphi$ für Runge-Kutta Verfahren:


$\displaystyle \varphi(t,v,h)$ $\displaystyle =$ $\displaystyle \sum_{i=1}^m \gamma_ik_i(t,v,h)$  
$\displaystyle k_1(t,v,h)$ $\displaystyle =$ $\displaystyle f(t,v)$  
$\displaystyle k_2(t,v,h)$ $\displaystyle =$ $\displaystyle f(t+\alpha_1h,v+h\beta_{21}k_1(t,v,h))$  
    $\displaystyle \vdots$  
$\displaystyle k_m(t,v,h)$ $\displaystyle =$ $\displaystyle f(t+\alpha_m h, v+h\sum_{j=1}^{m-1} \beta_{m,j}k_j(t,v,h))$  

Die Funktionen $ k_i(t,v,h)$ können also rekursiv durch

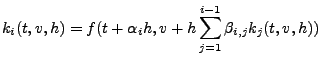
$\displaystyle k_i(t,v,h)=f(t+\alpha_ih, v+h\sum_{j=1}^{i-1} \beta_{i,j}k_j(t,v,h))$

bestimmt werden, wenn man $ \alpha_1=0$ setzt und $ \sum\limits_\emptyset= 0$ vereinbart.

Die zunächst unbekannten Koeffizienten $ \alpha_i, \gamma_i, \beta_{i,j}$ ordnet man in einem Koeffizientenschema an.

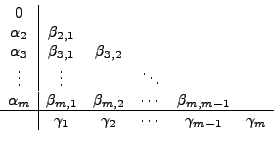
\begin{displaymath}\begin{array}{c\vert ccccc} 0 & & & & & \ \alpha_2 & \bet... ...1 & \gamma_2 & \cdots & \gamma_{m-1} & \gamma_m \ \end{array}\end{displaymath}

$ m$ heißt dabei Stufe des Runge-Kutta Verfahrens. Die bereits vorgestellten Verfahren lassen sich also kompakt beschreiben durch:

\begin{displaymath}\begin{array}{cc} \mbox{Euler Verfahren:} & \mbox{Verfahren ... ... 1 & 1 & \hline & 1/2 & 1/2 \end{array} \ \end{array}\end{displaymath}

Ein sehr bekanntes Verfahren der Stufe 4 und der Konsistenzordnung 4 ist das klassische Runge-Kutta Verfahren, das auch im Programm implementiert wurde:

\begin{displaymath}\begin{array}{c\vert cccc} 0 & & & & \ 1/2 & 1/2 & & & \\... ... 1& 0 & 0 & 1 & \hline & 1/6 & 1/3 & 1/3 & 1/6 \end{array}\end{displaymath}
Dies liefert den folgenden Algorithmus:
  1. $ j=0$
  2. $ t_{j+1} = t_j + h$
  3. Wenn $ t_{j+1} > t_{end}$ dann STOP, sonst weiter bei Schritt 4
  4. $ k_1 =f(t_j,u_j)$
  5. $ k_2 =f(t_j+h/2,u_j+h/2\cdot k_1)$
  6. $ k_3 =f(t_j+h/2,u_j+h/2\cdot k_2)$
  7. $ k_4 =f(t_j+h,u_j+h\cdot k_3)$
  8. $ u_{j+1}=u_j + h/6 \cdot ( k_1 + 2 k_2 + 2 k_3 + k_4 )$
  9. $ j=j+1$ und weiter bei Schritt 2

Man sieht sofort, dass dieser Algorithmus in jedem Schritt vier Auswertungen der Funktion $ f$ benötigt. Jedoch ist dieses Verfahren, wie bereits erwähnt, von der Konsistenzordnung 4.

Mit dem folgenden Programm kann man nun die vorgestellten Verfahren testen. Nach Eingabe der Anfangswertaufgabe und der Wahl der Schrittweite werden zunächst alle drei Verfahren durchgeführt. Anschließend kann man durch geeignete Einstellungen die Verfahren untereinander vergleichen oder den Konvergenzfehler darstellen, falls die Lösung explizit bekannt ist.

 

 Top