Ausgleichsprobleme
Das lineare Ausgleichsproblem
Gegeben sei eine reelle Funktion 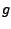 die neben der
Variablen 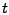 noch von einem unbekannten Vektor
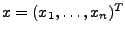 abhängt. Dabei habe
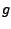 die Gestalt
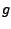 hängt also linear von den Komponenten
von hängt also linear von den Komponenten
von 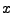 ab. ab.
Man kann nun z.B. durch ein Experiment versuchen die unbekannten
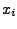 zu bestimmen. Dafür macht man zu bestimmen. Dafür macht man
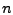 Beobachtungen, d.h. man notiert sich zu
jedem getesteten Beobachtungen, d.h. man notiert sich zu
jedem getesteten 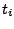 den Ausgang den Ausgang 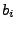 des Experiments. Man erhält dann ein lineares
Gleichungssystem in den
des Experiments. Man erhält dann ein lineares
Gleichungssystem in den 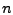 Unbekannten: Unbekannten:
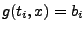 für 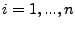
beziehungsweise
Schreibt man
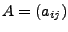 mit mit
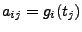 , so kann man das Problem auch
als , so kann man das Problem auch
als 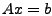 darstellen. Dieses lineare
Gleichungssystem kann genau dann eindeutig gelöst werden, wenn
der Rang von darstellen. Dieses lineare
Gleichungssystem kann genau dann eindeutig gelöst werden, wenn
der Rang von 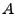 voll ist, d.h. wenn er voll ist, d.h. wenn er 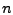 beträgt.
beträgt.
Hat man dagegen mehr Beobachtungen gemacht als man Parameter
hat, so wird das entstandene lineare Gleichungssystem wegen
Messfehlern im Allgemeinen keine Lösung mehr besitzen. Liegen
also 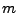 Messungen vor, wobei Messungen vor, wobei 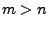 sei, erhält man wieder ein Gleichungssystem der
Form sei, erhält man wieder ein Gleichungssystem der
Form 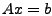 , aber mit , aber mit
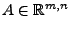 und und
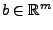 . In diesem Falle kann man
aber nach einer Lösung fragen, die die Messdaten in einem
gewissen Sinne noch ganz gut trifft (salopp also . In diesem Falle kann man
aber nach einer Lösung fragen, die die Messdaten in einem
gewissen Sinne noch ganz gut trifft (salopp also
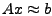 erfüllt). Als geeignetes
Maß hat sich erwiesen, die Differenz von erfüllt). Als geeignetes
Maß hat sich erwiesen, die Differenz von 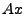 und
und 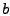 im Sinne der euklidischen Norm auf dem im Sinne der euklidischen Norm auf dem
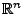 möglichst klein zu
bekommen. Der Differenzvektor möglichst klein zu
bekommen. Der Differenzvektor 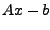 heißt
Residuum. Das Ziel ist also eine Lösung zu folgendem
Problem zu bestimmen: heißt
Residuum. Das Ziel ist also eine Lösung zu folgendem
Problem zu bestimmen:
minimiere 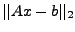
über alle 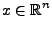
Da Quadrieren das Problem nicht verändert, betrachtet man:
minimiere 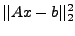
über alle 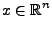
Dieses Problem nennt man das lineare Ausgleichsproblem. Die
Lösung kann man mittels der QR-Zerlegung von
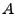 finden. Man stellt dabei 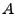
als Produkt einer orthogonalen Matrix
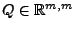 und einer 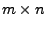 -Matrix
dar, deren oberer Teil aus einer oberen Dreiecksmatrix
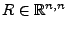 besteht:
Weil orthogonale Matrizen die euklidische Norm invariant lassen,
gilt
wenn man den Vektor
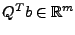 mit
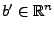 und
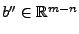 wie folgt
partitioniert:
Daran sieht man, dass genau das 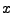 den Term
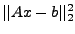 minimiert,
welches 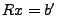 löst. Das Ergebnis schreibt man
auch als 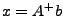 , wobei
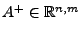 die sog.
Pseudoinverse von 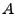 ist. Die minimale
Residuumsnorm beträgt in diesem Fall
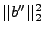 .
Das nichtlineare Ausgleichsproblem
Hierbei geht es allgemein um die Minimierung einer Funktion
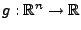 . Allerdings
ist bekannt dass 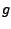 die Form
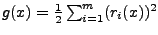 hat.
Die Komponenten der Abbildung
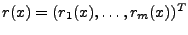 heißen
Residuen. Wieder sollen also die unbekannten
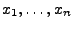 so bestimmt werden, dass
dieser Term möglichst klein ist. Dies ist im Allgemeinen nicht
mehr direkt zu lösen, sondern man muss mit iterativen
Methoden arbeiten, die ausgehend von einer
Näherungslösung 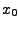 eine Folge
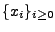 erzeugen, die hoffentlich
gegen eine Lösung des Problems konvergiert.
Das Gauß-Newton-Verfahren
Anpassung von Funktionen
Möchte man eine nichtlineare Funktion 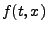
durch gegebene Messpunkte
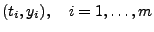 laufen lassen,
so ist dies sicherlich nicht immer möglich. Aber man kann
fordern, dass an jedem Punkt 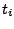 die Differenz von
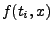 und 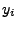
möglichst klein sein soll.
Genauer: Es ist das
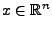 gesucht, für das der
Term gesucht, für das der
Term
minimal wird. Mit
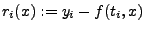 ist dies also ein
nichtlineares Ausgleichsproblem wie im vorherigen Abschnitt.
Das folgende Programm ermöglicht eine solche Anpassung von
einer beliebigen Funktion an beliebige Daten. Als Methoden stehen
sowohl das ungedämpfte als auch das gedämpfte
Gauß-Newton-Verfahren zur Verfügung. Schafft das Programm
keine Anpassung, steckt die Folge
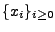 also z.B. in einem lokalen
Minimum fest, so hilft es meist nur die Anfangsvorgabe zu
verbessern. also z.B. in einem lokalen
Minimum fest, so hilft es meist nur die Anfangsvorgabe zu
verbessern.
|