Mehrschrittverfahren

Theoretischer Hintergrund

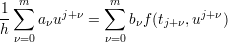
Ist

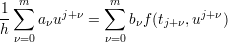
m m 1-∑ a uj+ ν = ∑ b f(t ,uj+ ν) h ν ν j+ν ν=0 ν=0

ein lineares Mehrschrittverfahren zur Lösung von Anfangswertproblemen, so ist die Konsistenzordnung des Verfahrens p, wenn die Koeffizienten a_ν,b_ν folgende Gleichungen erfüllen

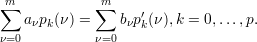∑m ∑m aνpk (ν) = bνp′k(ν),k = 0,...,p. ν=0 ν=0

(1)

Dabei ist p_k(ν) = 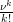k
νk! .

Um die triviale Lösung auszuschließen und die Lösung eindeutig zu machen, fordert man zusätzlich

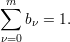m ∑ bν = 1. ν=0

(2)

Es gilt der folgende Satz

Satz.

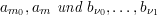
I): Alle Koeffizienten seien Null außer $am0,am und bν0,...,bν1$
mit m₀ < m. Dann sind (1) und (2) mit p = ν₁ − ν₀ + 1 eindeutig lösbar und p gibt die Konsistenzordnung des Verfahrens an.
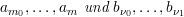
II): Alle Koeffizienten seien Null außer $am0,...,am und bν0,...,bν1$
mit m₀ ≤ ν₀ ≤ ν₁ ≤ m. Dann sind (1) und (2) mit p = m−m₀+ν₁−ν₀ eindeutig lösbar und p gibt die Konsistenzordnung des Verfahrens an.

Beispiele

I)

a): m₀ = m − 1,ν₀ = 0,ν₁ = m − 1 Adams-Bashforth
b): m₀ = m − 1,ν₀ = 0,ν₁ = m Adams-Moulton
c): m₀ = m − 2,ν₀ = 0,ν₁ = m − 1 Nyström
d): m₀ = m − 2,ν₀ = 0,ν₁ = m Milne-Simpson

II)

a): m₀ = 0,ν₀ = ν₁ = m rückwärtige Differenzenformeln (BDF)
b): m₀ = 0,ν₀ = ν₁ = m − 1 Mittelpunktsregel