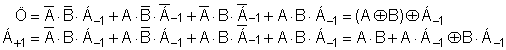3.2.3. Az aritmetikai műveletek visszavezetése logikai műveleteket végrehajtó áramkörökre
Azt már láttuk, hogy az összes aritmetikai művelet végrehajtásának 2-es számrendszerbeli algoritmusa visszavezethető fixpontos számokkal végzett bitenként történő összeadásra és shiftelésre. Ezért ahhoz, hogy bármilyen aritmetikai művelet végrehajtható legyen Boole algebrai műveleteket modellező áramkörökkel, elég ezt megmutatni az 1-bites összeadás esetére.
Jelölje A és B a két 1-bites összeadandót, Á-1 az összeadás előző helyiértékéről származó átvitelt, az összeadás eredményét pedig Ö. Ha az összeadás során újabb átvitel képződik, akkor ez legyen Á+1. Ekkor az 1-bites összeadó Boole algebrai igazságtáblázata, illetve az ebből levezetett és csak két logikai alapműveletet tartalmazó függvény a következő lesz:
|
KIINDULÓ ADATOK |
EREDMÉNY |
|||
|
A |
B |
Á-1 |
Ö |
Á+1 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |